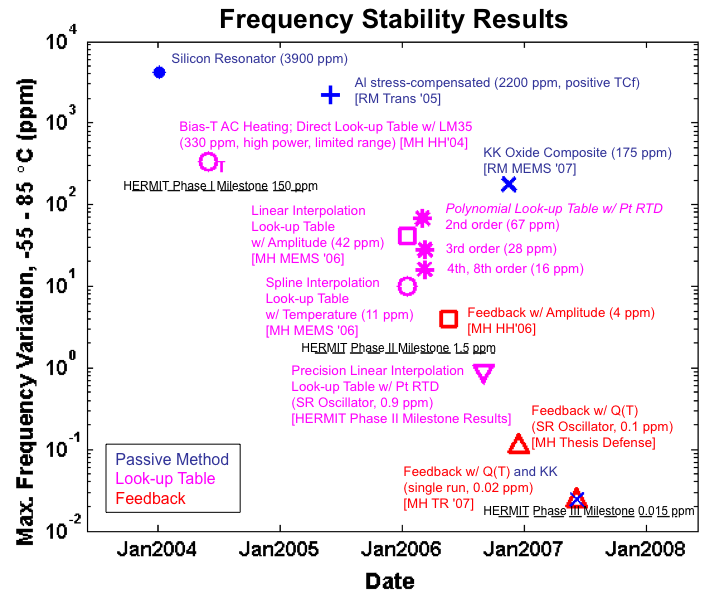
References:
[1] R. N. Candler, M. A. Hopcroft, B. Kim, W. T. Park, R. Melamud, M. Agarwal, G. Yama, A. Partridge, M. Lutz, and T. W. Kenny, "Long-Term and Accelerated Life Testing of a Novel Single-Wafer Vacuum Encapsulation for MEMS Resonators," Journal of Microelectromechanical Systems, vol. 15, pp. 1446-1456, 2006.
[2] B. Kim, R. N. Candler, M. A. Hopcroft, M. Agarwal, W.-T. Park, and T. W. Kenny, "Frequency stability of wafer-scale film encapsulated silicon based MEMS resonators," Sensors and Actuators A: Physical, vol. 136, pp. 125-131, 2007.
[3] J.-h. Jeong, S.-h. Chung, S.-H. Lee, and D. Kwon, "Evaluation of elastic properties and temperature effects in Si thin films using an electrostatic microresonator," Journal of Microelectromechanical Systems, vol. 12, 2003.
[4] K. Wang and C. T.-C. Nguyen, "High-order medium frequency micromechanical electronic filters," Journal of Microelectromechanical Systems, vol. 8, 1999.
[5] W.-T. Hsu and C. T.-C. Nguyen, "Geometric stress compensation for enhanced thermal stability in micromechanical resonators," Ultrasonics Symposium, 1998.
[6] R. Melamud, et al., "Effects of stress on the temperature coefficient of frequency in double clamped resonators," presented at TRANSDUCERS '05, Solid-State Sensors, Actuators and Microsystems, 2005. The 13th International Conference on, Seoul, ROK, 2005.
[7] R. Melamud, et al., "Composite Flexural Mode Resonator with Reduced Temperature Coefficient of Frequency," presented at Solid-State Sensor, Actuator and Microsystems Workshop, 2006. Technical Digest, IEEE., Hilton Head, SC USA, 2006 (Hilton Head '06).
[8] R. N. Candler, et al., "Investigation of Energy Loss Mechanisms in Micromechanical Resonators," presented at the 12th International Conference on Solid-State Sensors, Actuators and Microsystems, 2003 (TRANSDUCERS '03), Boston, MA USA, 2003.
[9] B. Kim, et al., "Temperature Dependence of Quality Factor in MEMS Resonators," presented at Micro Electro Mechanical Systems, 2006, 19th IEEE International Conference on (MEMS '06). Istanbul, Turkey, 2006.
[10] M. A. Hopcroft, B. Kim, S. Chandorkar, R. Melamud, M. Agarwal, C. M. Jha, G. Bahl, J. Salvia, H. Mehta, H. K. Lee, R. N. Candler, and T. W. Kenny, "Using the temperature dependence of resonator quality factor as a thermometer," Applied Physics Letters, vol. 91, pp. 013505-3, 2007.
[11] W.-T. Hsu, et al., "Mechanically temperature-compensated flexural-mode micromechanical resonators," IEDM, 2000.
[12] Corning, Inc. Part C4700 Datasheet
Also see here for related publications.
|